
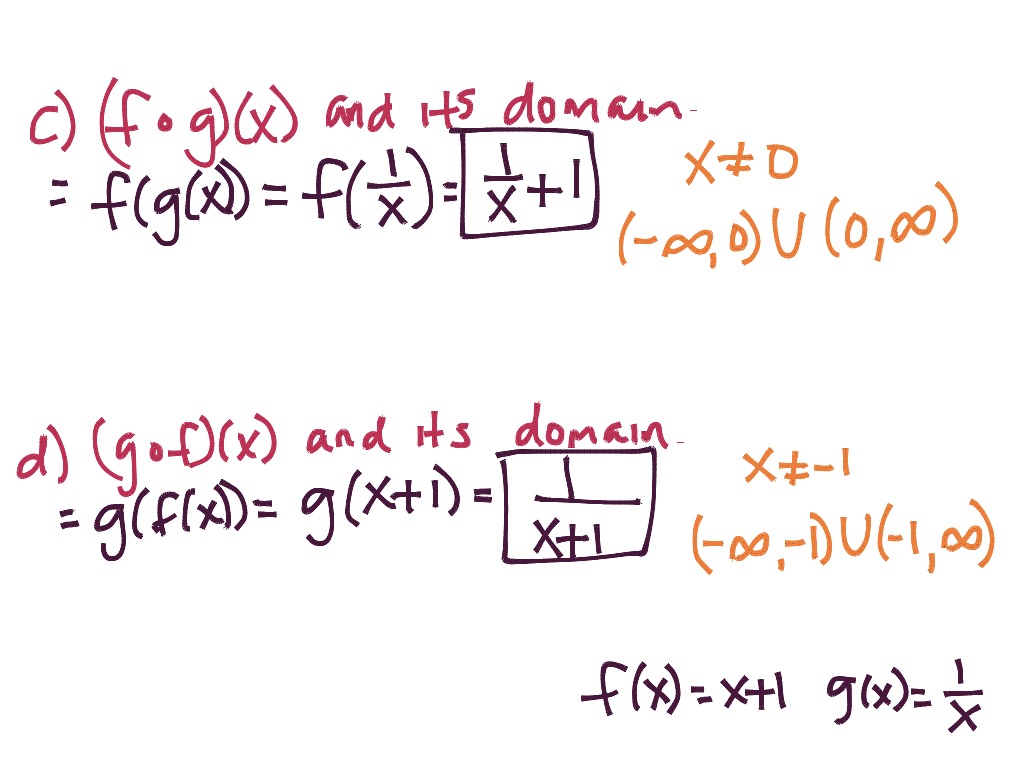
Composition is a binary operation that takes two functions and forms a new function, much as addition or multiplication takes two numbers and gives a new number. We do this by performing the operations with the function outputs, defining the result as the. Another way is to carry out the usual algebraic operations on functions, such as addition, subtraction, multiplication and division. Function composition is only one way to combine existing functions. We use this operator mainly when we wish to emphasize the relationship between the functions themselves without referring to any particular input value. Combining Functions Using Algebraic Operations. The open circle symbol \(\circ\) is called the composition operator. For example, if f (x) 2x + 1 and g (x) x - 3, then the doamins of f+g, f-g, and fg are all real numbers. The quotient f/g is not defined at values of x where g is equal to 0. The main ideas are that the limit of a product is the product of the limits, and that the limit of a quotient is the quotient of the limits, provided the denominators limit isnt zero. Generally, an arithmetic combination of two functions f and g at any x that is in the domain of both f and g, with one exception.
#Combining functions how to
We read the left-hand side as“\(f\) composed with \(g\) at \(x\),” and the right-hand side as“\(f\) of \(g\) of \(x\).”The two sides of the equation have the same mathematical meaning and are equal. In this video, we learn how to find the limit of combined functions using algebraic properties of limits. We represent this combination by the following notation: The resulting function is known as a composite function.

The process of combining functions so that the output of one function becomes the input of another is known as a composition of functions. When we wanted to compute a heating cost from a day of the year, we created a new function that takes a day as input and yields a cost as output. When two functions combine in a way that the output of one function becomes. Performing algebraic operations on functions combines them into a new function, but we can also create functions by composing functions. The mapping of elements of A to C is the basic concept of Composition of functions. The slope is the change in y for each unit change in x. A composite function is defined as using the output of one function (generally f(x)) as input for another function (generally g(x)). One of the distinguishing features of a line is its slope. Given two functions, say f(x) and g(x), to add (f+g)(x) or f(x) + g(x) or to subtract (f - g)(x) or f(x) - g(x. As suggested by Figure 1.1.1, the graph of any linear function is a line. Learn how to add or subtract two functions. \]Ĭreate a Function by Composition of Functions Figure 1.1.1: These linear functions are increasing or decreasing on (, ) and one function is a horizontal line.


 0 kommentar(er)
0 kommentar(er)
